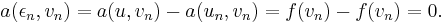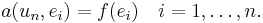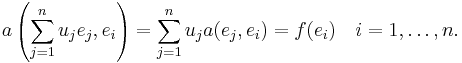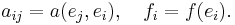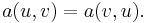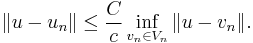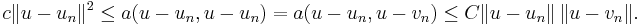Galerkin method

In mathematics, in the area of numerical analysis, Galerkin methods are a class of methods for converting a continuous operator problem (such as a differential equation) to a discrete problem. In principle, it is the equivalent of applying the method of variation of parameters to a function space, by converting the equation to a weak formulation. Typically one then applies some constraints on the function space to characterize the space with a finite set of basis functions. Often when using a Galerkin method one also gives the name along with typical approximation methods used, such as Petrov–Galerkin method (after Alexander G. Petrov) or Ritz–Galerkin method^[1] (after Walther Ritz).

The approach is credited to the Russian mathematician Boris Galerkin.

Examples of Galerkin methods are:

The Galerkin method of weighted residuals, the most common method of calculating the global stiffness matrix in the finite element method^[2],^[3]
Boundary element method for solving integral equations
Krylov subspace methods ^[4]

1 Introduction with an abstract problem
2 Analysis of Galerkin methods
- 2.1 Well-posedness of the Galerkin equation
- 2.2 Quasi-best approximation (Céa's lemma)
  - 2.2.1 Proof
3 Application to the finite element method for Poisson's equation
4 Application to the analysis of the conjugate gradient method
5 References
6 External links

Introduction with an abstract problem

A problem in weak formulation

Let us introduce Galerkin's method with an abstract problem posed as a weak formulation on a Hilbert space, $V$ , namely,

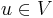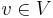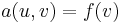find $u\in V$ such that for all $v\in V$ , $a(u,v) = f(v)$ .

Here, 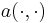$a(\cdot,\cdot)$ is a bilinear form (the exact requirements on 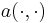$a(\cdot,\cdot)$ will be specified later) and $f$ is a bounded linear functional on $V$ .

Galerkin discretization

Choose a subspace 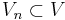$V_n \subset V$ of dimension n and solve the projected problem:

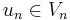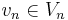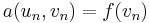Find $u_n\in V_n$ such that for all $v_n\in V_n$ , $a(u_n,v_n) = f(v_n)$ .

We call this the Galerkin equation. Notice that the equation has remained unchanged and only the spaces have changed.

Galerkin orthogonality

The key property of the Galerkin approach is that the error is orthogonal to the chosen subspaces. Since 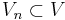$V_n \subset V$ , we can use 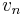$v_n$ as a test vector in the original equation. Subtracting the two, we get the Galerkin orthogonality relation for the error, 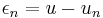$\epsilon_n = u-u_n$ which is the error between the solution of the original problem, $u$ , and the solution of the Galerkin equation, $u_n$

$a(\epsilon_n, v_n) = a(u,v_n) - a(u_n, v_n) = f(v_n) - f(v_n) = 0.$

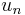
Matrix form

Since the aim of Galerkin's method is the production of a linear system of equations, we build its matrix form, which can be used to compute the solution by a computer program.

Let 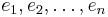$e_1, e_2,\ldots,e_n$ be a basis for 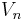$V_n$ . Then, it is sufficient to use these in turn for testing the Galerkin equation, i.e.: find 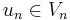$u_n \in V_n$ such that

$a(u_n, e_i) = f(e_i) \quad i=1,\ldots,n.$

We expand 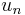$u_n$ in respect to this basis, 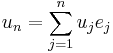$u_n = \sum_{j=1}^n u_je_j$ and insert it into the equation above, to obtain

$a\left(\sum_{j=1}^n u_je_j, e_i\right) = \sum_{j=1}^n u_j a(e_j, e_i) = f(e_i) \quad i=1,\ldots,n.$

This previous equation is actually a linear system of equations 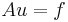$Au=f$ , where

$a_{ij} = a(e_j, e_i), \quad f_i = f(e_i).$

Symmetry of the matrix

Due to the definition of the matrix entries, the matrix of the Galerkin equation is symmetric if and only if the bilinear form 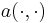$a(\cdot,\cdot)$ is symmetric.

Analysis of Galerkin methods

Here, we will restrict ourselves to symmetric bilinear forms, that is

$a(u,v) = a(v,u).$

While this is not really a restriction of Galerkin methods, the application of the standard theory becomes much simpler. Furthermore, a Petrov-Galerkin method may be required in the nonsymmetric case.

The analysis of these methods proceeds in two steps. First, we will show that the Galerkin equation is a well-posed problem in the sense of Hadamard and therefore admits a unique solution. In the second step, we study the quality of approximation of the Galerkin solution 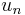$u_n$ .

The analysis will mostly rest on two properties of the bilinear form, namely

Boundedness: for all 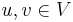$u,v\in V$ holds

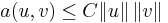$a(u,v) \le C \|u\|\, \|v\|$ for some constant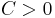 $C>0$
Ellipticity: for all 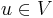$u\in V$ holds

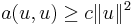$a(u,u) \ge c \|u\|^2$ for some constant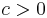 $c>0$

By the Lax-Milgram theorem (see weak formulation), these two conditions imply well-posedness of the original problem in weak formulation. All norms in the following sections will be norms for which the above inequalities hold (these norms are often called an energy norm).

Well-posedness of the Galerkin equation

Since 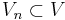$V_n \subset V$ , boundedness and ellipticity of the bilinear form apply to 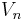$V_n$ . Therefore, the well-posedness of the Galerkin problem is actually inherited from the well-posedness of the original problem.

Quasi-best approximation (Céa's lemma)

Main article: Céa's lemma

The error 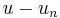$u-u_n$ between the original and the Galerkin solution admits the estimate

$\|u-u_n\| \le \frac{C}{c} \inf_{v_n\in V_n} \|u-v_n\|.$

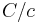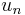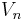This means, that up to the constant $C/c$ , the Galerkin solution $u_n$ is as close to the original solution $u$ as any other vector in $V_n$ . In particular, it will be sufficient to study approximation by spaces 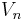$V_n$ , completely forgetting about the equation being solved.

Proof

Since the proof is very simple and the basic principle behind all Galerkin methods, we include it here: by ellipticity and boundedness of the bilinear form (inequalities) and Galerkin orthogonality (equals sign in the middle), we have for arbitrary 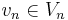$v_n\in V_n$ :

$c\|u-u_n\|^2 \le a(u-u_n, u-u_n) = a(u-u_n, u-v_n) \le C \|u-u_n\| \, \|u-v_n\|.$

Dividing by 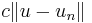$c \|u-u_n\|$ and taking the infimum over all possible 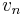$v_n$ yields the lemma.

Application to the finite element method for Poisson's equation

Application to the analysis of the conjugate gradient method

References

^ A. Ern, J.L. Guermond, Theory and practice of finite elements, Springer, 2004, ISBN 0-3872-0574-8
^ S. Brenner, R. L. Scott, The Mathematical Theory of Finite Element Methods, 2nd edition, Springer, 2005, ISBN 0-3879-5451-1
^ P. G. Ciarlet, The Finite Element Method for Elliptic Problems, North-Holland, 1978, ISBN 0-4448-5028-7
^ Y. Saad, Iterative Methods for Sparse Linear Systems, 2nd edition, SIAM, 2003, ISBN 0-8987-1534-2

External links

Areas of mathematics

Areas	Arithmetic · Algebra (elementary – linear – multilinear – abstract) · Geometry (Discrete geometry – Algebraic geometry – Differential geometry) · Calculus/Analysis · Set theory · Logic · Category theory · Number theory · Combinatorics · Graph theory · Topology · Lie theory · Differential equations/Dynamical systems · Mathematical physics · Numerical analysis · Computation · Information theory · Probability · Statistics · Optimization · Control theory · Game theory

Divisions	Pure mathematics · Applied mathematics · Discrete mathematics · Computational mathematics

Category · Mathematics portal · Outline · Lists